Question

What's the length of PS, QS, and area of PQR?

Answer 1

First, notice the following right triangle that we can get with the vertices Q,S and P:

then, we can find PS and QS using the trigonometric functions sine and cosine:

`\begin{gathered} \sin (62.58)=\frac{\text{opposite side}}{hypotenuse}=(PS)/(4.5) \\ \Rightarrow PS=4.5\cdot\sin (62.58)=3.99 \\ \cos (62.58)=\frac{\text{adjacent side}}{hypotenuse}=(QS)/(4.5) \\ \Rightarrow QS=4.5\cdot\cos (62.58)=2.07 \end{gathered}`

therefore, PS = 3.99 and QS = 2.07

Now, notice that the base of the triangle PQR is:

`QR=QS+SR`

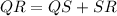
since we already know that SR = 5, we have that the base of the triangle is:

`QR=2.07+5=7.07`

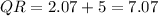
Now we can find the area of the triangle PQR:

`A_{\Delta\text{PQR}}=\frac{\text{base}\cdot\text{height}}{2}=(QR\cdot PS)/(2)=(7.07\cdot3.99)/(2)=(28.21)/(2)=14.11`

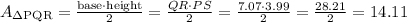
therefore, the area of triangle PQR is 14.11 u^2