Given:
Number of sample (n) = 50
mean = 300
standard deviation (s) = 47
confidence level = 95%
The margin of error (MOE) can be calculated using the formula:
![\text{MOE = z }*\text{ }\frac{s}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/4pcr1r193mh36am0fn8risftv27dqszwmh.png)
Where z is the z-score at the given confidence level
At 95% confidence level, the z-score is 1.960
The margin of error is thus:
![\begin{gathered} \text{MOE =1.96 }*\frac{47}{\sqrt[]{50}} \\ =\text{ 13.0277} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y5qfn5hkefncc6uovnamikiqkrnxfe4zf7.png)
The formula to calculate the confidence interval is:
![\begin{gathered} CI=\operatorname{mean}\pm z\frac{s}{\sqrt[]{n}}^{} \\ CI\text{ = mean }\pm\text{ margin of error} \end{gathered}]()
Where :
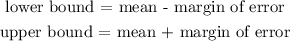
Substituting:

Hence, if we to randomly sample from this population 100 times. The probability of having a score between 287 and 313 is 0.95