Solution:
Given:
A parallelogram with;
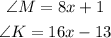
In a parallelogram, the angles on the same side of the transversal are supplementary, which means they add up to 180 degrees.
Hence,
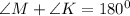
Thus,

To get the measure of angle K, we substitute the value of x gotten.
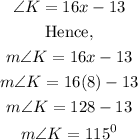
Therefore, the measure of angle K in the parallelogram is 115 degrees.