In order to get the surface area of a hemisphere, let's determine its radius first.
Based on the question, the circumference of a great circle is 40.8 inches. Since circumference = 2πr, then 40.8 inches = 2πr. From this, we can solve for the radius.
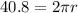
To solve for the radius, divide both sides of the equation by 2π. Use π = 3.14159
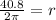

Therefore, the length of the radius is 6.4935 inches.
Now that we have the radius, let's calculate the surface area of the hemisphere. The formula is:

Let's plug into the formula r = 6.4935 inches and π = 3.14159
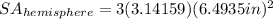
Then, solve.
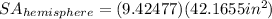
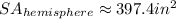
Therefore, the surface area of the hemisphere is approximately 397.4 square inches.