Given data:
* The height of the window is 10 m.
* The angle of the incident velocity with respect to the horizontal is 60 degree.
Solution:
(a). The height of the projectile in terms of the initial velocity is,
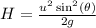
where u is the initial velocity, g is the acceleration due to gravity, and
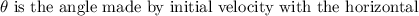
Substituting the known values,
The initial velocity of the projectile is,
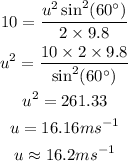
Thus, the initial velocity of the bag is 16.2 m/s at an angle of 60 degree to the ground.
(b). The horizontal range of bag is,
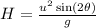
Substituting the known values,
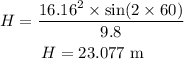
The position of the bag from the house is,
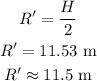
Thus, the lad is standing at the distance of 11.5 m from the house.