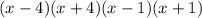We can make a u-substitution to make it into a quadratic.
Let
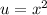
Performing this substitution, we have:

Now, taking it back to "x", we have:
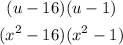
We can further break it down by using the rule:
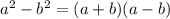
So, let's factor it out completely:
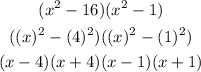
Thus, the fully factored form is: