Since the triangles ΔQRS and ΔTUV, their corresponding sides are also congruent, this means that
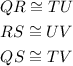
Since QS and TV are congruent, this means that they have the same measures, therefore
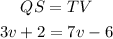
Solving this equation for v, we have
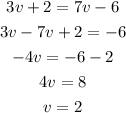
Using this value for v in our expression for the sides, we have
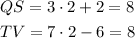
Both sides are equal to 8.