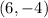Question

Name the coordinates of point H after it is reflected over the x-axis and then the y-axis. The initial directions are in the pic below.

Answer 1

We have a point H = (x, y):

0. after H is reflected over the x-axis, we have H' = (x, -y),

,

1. after H' is reflected over the y-axis, we have H'' = (-x, -y).

In this case, we have the point:

`H=(x,y)=(-6,4).`

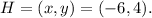
After the two reflections, we get the point:

`H^(\prime\prime)=(x^(\prime)^(\prime),y^(\prime)^(\prime))=(-x,-y)=(-(-6),-4)=(6,-4)\text{.}`

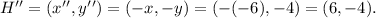
Answer

The coordinates of point H after it is reflected over the x-axis and then the y-axis are:

`(6,-4)`