Given:
a.) You deposit $4000 in an account earning 8% interest compounded monthly.
Question: How much will you have in the account in 15 years?
We will be using the following formula:
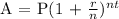
Where,
A=final amount
P=initial principal balance = $ 4,000
r=interest rate = 8% = 8/100 = 0.08
n=number of times interest applied per time period = monthly = 12
t=number of time periods elapsed = 15 years
We get,
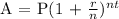
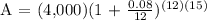
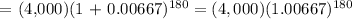
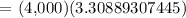

Therefore, in 15 years, you will have $13,235.57 in your account.