Answer
The answer is 7,911,000,000
EXPLANATION
Problem Statement
The question tells us that the world's population is modeled by the formula:
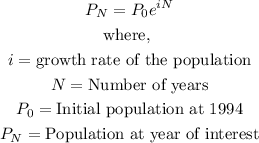
Solution
To solve this question, we simply need to plug in all the values given to us. That is,
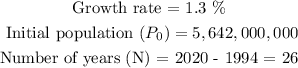
Thus, we can find the estimated world population in year 2020 as follows:
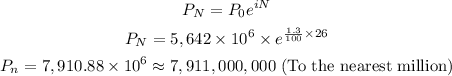
Final Answer
The answer is 7,911,000,000