Question

A 35 kg crate is at rest on the floor. A man attempts to push it across the floor by applying a 100 N force horizontally. (a) Take the coefficient of static friction between the crate and floor to be 0.37 and show that the crate does not move. (b) A second man helps by pulling up on the crate. Calculate the minimum vertical force he must apply so that the crate starts to move across the floor. (c) If the second man applies a horizontal rather than a vertical force, what minimum force, in addition to the 100 N force of the first man, must he exert to get the crate started?

Answer 1

eGiven:

The mass of the crate is,

`m=35\text{ kg}`

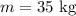
The coefficient of friction between the floor and the crate is,

`\mu=0.37`

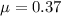
The force applied by the man is ,

`F=100\text{ N}`

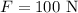
The frictional force on the crate is,

`\begin{gathered} f=\mu mg \\ =0.37*35*9.8 \\ =126.9N \end{gathered}`

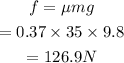
Here the applied force is less than the frictional force. so the crate will not move.

part b

if the other person applies force,

`F_2`

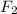
WE CAN WRITE the vertical force,

`F_N=mg-F_2`

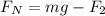
the frictional force is then,

`f=\mu(mg-F_2)`

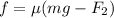
we can say,

`\begin{gathered} 100>f \\ 100>0.37(35*9.8-F_2) \\ F_2>72.7\text{ N} \end{gathered}`

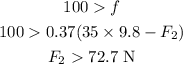
part c

the maximum frictional force is as calculated above,

`f_(\max )=126.9\text{N}`

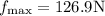
the extra force by the other person if added we can write,

`\begin{gathered} F_1+F_2>126.9 \\ 100+F_2>126.9 \\ F_2>26.9\text{ N} \end{gathered}`

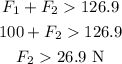
hence the added force in26.9 N