Question

Approximately how many minutes until the 1000 g initial sample decays to 10 g (half-life is 3 minutes)?

Answer 1

The half-life formula is given by

`N(t)=N_0((1)/(2))^{(t)/(tm)}`

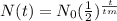
where N(t) is the final amount, N_0 is the initial quantity, t is the elapsed time and tmis the half life of the substance.

In our case,

`\begin{gathered} N(3)=10g \\ N_0=1000g \\ t_m=3\text{ minutes} \end{gathered}`

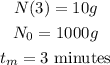
and we need to find t. By substituting these values into the formula, we have

`10=1000((1)/(2))^{(t)/(3)}`

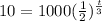
which gives

`\begin{gathered} (10)/(1000)=((1)/(2))^{(t)/(3)} \\ 0.01=((1)/(2))^{(t)/(3)} \end{gathered}`

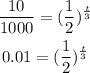
By applying natural logarithm to both sides ,we have

`\ln (0.01)=(t)/(3)\ln ((1)/(2))`

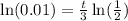
which gives

`\begin{gathered} -4.605=(t)/(3)(-0.693) \\ \text{then} \\ (t)/(3)=(-4.605)/(-0.693) \\ (t)/(3)=6.6438 \end{gathered}`

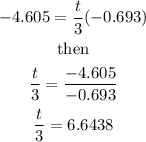
Therefore, the elapsed time t is given by

`\begin{gathered} t=3*6.6438 \\ t=19.93\text{ } \end{gathered}`

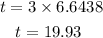
Therefore, the answer is 19.93 minutes.