Question

What is the value of each variable?Xy60°16X =y0084:: 8√2:: 8√3:: 4√2:: 4√3

Answer 1

GIVEN:

We are given a right angled triangle with sides and angles as indicated.

Required;

We are required to use the information given to calculate the missing sides, x and y.

Step-by-step solution:

We have a right angled triangle with the reference angle given as 60 degrees. Therefore, the sides will be labelled as follows;

`\begin{gathered} x=opposite \\ y=adjacent \\ 16=hypotenuse \end{gathered}`

To calculate the side labeled x, we would use the trig ratio which is,

`sin\theta=(opposite)/(hypotenuse)`

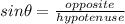
Therefore;

`sin60\degree=(x)/(16)`

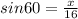
We shall apply the values of special angles. For a trigonometric calculation with right angled triangles,

`sin60\degree=(√(3))/(2)`

The equation can now be refined and written as follows;

`(√(3))/(2)=(x)/(16)`

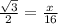
Now we cross multiply;

`\begin{gathered} (16√(3))/(2)=x \\ \\ 8√(3)=x \end{gathered}`

Next we calculate the value of y. We shall use the ratio;

`cos\theta=(adjacent)/(hypotenuse)`

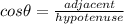
Hence;

`cos60\degree=(y)/(16)`

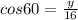
The cosine of 60 degrees is,

`cos60\degree=(1)/(2)`

We substitute this into the equation above;

`\begin{gathered} (1)/(2)=(y)/(16) \\ \\ Cross\text{ }multiply; \\ \\ (16*1)/(2)=y \\ \\ 8=y \end{gathered}`

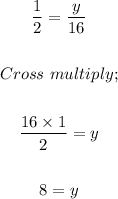
Therefore the missing sides are;

ANSWER:

`\begin{gathered} x=8√(3) \\ \\ y=8 \end{gathered}`

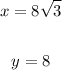
x = 8√3

y = 8