Question

Find an equation of the ellipse having a major axis of length 8 and foci at (-4, 4) and (-4,0).

Answer 1

Hello there. To solve this question, we'll have to remember some properties about ellipses.

Given that the major axis length of the ellipse is 8 and its foci are at (-4, 4) and (-4, 0), we already have two informations that guides us into the form we're looking for.

First, the equation of an ellipse is given as

`((x-x_0))/(a^2)+((y-y_0))/(b^2)=1`

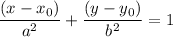
Where (x0, y0) are the coordinates of the center of the ellipse, a and b are the major and minor axis (not respectively, because it depends whether the axis of symmetry of the ellipse is a x or y line).

We find the foci coordinates using the values of a and b, but in this case, as they were given, we do the opposite.

Let's start drawing the foci:

Since the foci are aligned as in a vertical line, we know that this ellipse has a major axis parallel to the y-axis.

Its center is the midpoint of the segment joining the foci, that is, the ordered pair (xm, ym) such that

`\begin{gathered} x_m=(-4+(-4))/(2)=(-8)/(2)=-4 \\ \\ y_m=(4+0)/(2)=(4)/(2)=2 \\ \end{gathered}`

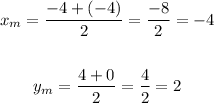
Hence the center is at (-4, 2).

In the case of the major axis being parallel to the y-axis, we write the equation of the ellipse as follows:

`((y-y_0))/(a^2)+((x-x_0))/(b^2)=1`

Finally, we have to determine the value of a.

We know that is the semi-major axis of the ellipse, hence it has half the length of the major axis. Since it was given to be 8, we have that

`a=(8)/(2)=4`

And we determine the value of b by using the following rule for ellipses:

Therefore we get that c is the distance between the foci and the center, in this case it is simply 2.

Plugging the values we found, we get

`\begin{gathered} 4^2=b^2+2^2 \\ \\ 16=b^2+4 \\ \\ b^2=12 \end{gathered}`

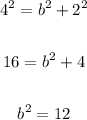
In this case, we can say that the semi-minor axis of this ellipse has a measure of 2sqrt(3), but as we only need the value squared, we plug it into the equation as:

`\begin{gathered} ((y-2)^2)/(16)+((x-(-4))^2)/(12)=1 \\ \\ \boxed{((y-2)^2)/(16)+((x+4)^2)/(12)=1} \end{gathered}`

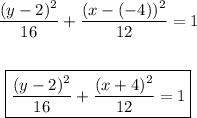
This is the answer to this question. You can see its graph in the following image: