We have to find the general solution to:
![3\cot \theta=-\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/d58tajodebqcpmbzmqnb8b2x1typ2zgfss.png)
We can start rearranging the equation:
![\begin{gathered} \cot \theta=-\frac{\sqrt[]{3}}{3} \\ (1)/(\tan\theta)=-\frac{\sqrt[]{3}}{3} \\ (1)/(\tan\theta)=-\frac{1}{\sqrt[]{3}} \\ \tan \theta=-\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o2t4tfe0sfuw7furyhtv666j89rov9e308.png)
We will have one solution per cycle of length π.
We calculate the solution for the first period as:
![\begin{gathered} \tan \theta=-\sqrt[]{3} \\ \theta=\arctan (-\sqrt[]{3}) \\ \theta=(2\pi)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gmg8r3unwveb09plbxsgc0f5fv9a8m3ry8.png)
We then can generalize for the other periods as:
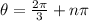
Answer: θ = 2π/3 + πn