To answer this question we will use the following formula for compounded daily interest:
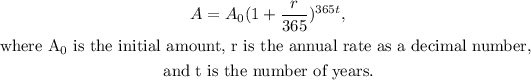
Substituting A₀=8700, A=12000, and r=0.02 we get:
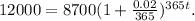
Dividing the above result by 8700 we get:
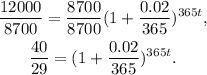
Applying the natural logarithm we get:
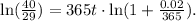
Finally, dividing the above equation by
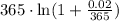
we get:
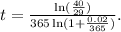
Therefore:
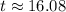
Answer: The value of the fund reaches $12,000 after 16.08 years.