Answer:
6.24 units
Step-by-step explanation:
Recall that the angle between a tangent AB and the radius, BO is always 90 degrees.
Therefore, triangle ABO is a right triangle.
Applying the Pythagorean Theorem:
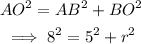
We solve the equation above for r:
![\begin{gathered} r^2=8^2-5^2 \\ r^2=64-25 \\ r^2=39 \\ r=\sqrt[]{39} \\ r\approx6.24 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tucpzw879qftwjxpujyzo30oavmab1wuai.png)
The length of the radius is approximately 6.24 units.