Question

A circle has a radius of 5 inches. Find the length of the arc intercepted by a central angle of 300 degrees. Round to the nearest hundredth of an inch.A circle has a radius of 5 inches. Find the length of the arc intercepted by a central angle of 300 degrees. Round to the nearest hundredth of an inch.choice:13.01 inches8.33 inches26.18 inches9.424.78 inches

Answer 1

3rd option: 26.18 inches

Explanation:

The length of the arc is calculated by a proportion between the circumference, which is the measure of the 360° of the circle, and the length of the 300°.

Therefore, the first thing is to calculate the circumference just like this:

`\begin{gathered} c=2\pi r \\ \\ \text{ We replacing} \\ \\ c=(2)(3.14)(5) \\ \\ c=31.415\text{ in} \end{gathered}`

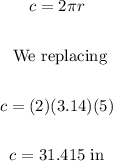
Now, if we calculate the length of the arc using the proportion, like this:

`\begin{gathered} \:(31.415)/(360)=(arc)/(300)\: \\ \\ arc=31.415\cdot(300)/(360) \\ \\ arc=26.18\text{ in} \end{gathered}`

Therefore, the correct answer is 3rd option: 26.18 inches