Question

A pinball machine is inclined at a 10 degree angle. A ball is shot through the machine and slides up. The 0.1 kg ball is hit and slides on the frictionless machine floor. What’s the ball acceleration? How far up can the ball roll until it stops and rolls back down if launched with a speed of 1 m/s?

Answer 1

Since there is no external force acting on the ball, the only force that generates acceleration is the weight force of the ball.

Since the ball is inclined in a 10° angle, the component of the weight that will generate acceleration in the direction of the movement is:

`\begin{gathered} F=m\cdot a \\ W\cdot\sin (10\degree)=m\cdot a \\ m\cdot g\cdot\sin (10\degree)=m\cdot a \\ g\cdot\sin (10\degree)=a \\ a=-9.8\cdot0.1736 \\ a=-1.7\text{ m/s2} \end{gathered}`

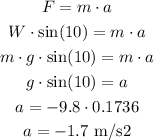
Therefore the ball acceleration is 1.7 m/s² down the ramp (opposing the initial movement).

Since the initial speed is 1 m/s and the final speed up the ramp is 0, we can use Torricelli's equation to find the displacement:

`\begin{gathered} V^2=V^2_0+2\cdot a\cdot d \\ 0=1^2+2\cdot(-1.7)\cdot d \\ 1-3.4d=0 \\ 3.4d=1 \\ d=(1)/(3.4)=0.2941\text{ m} \end{gathered}`

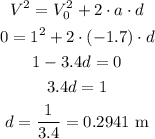
Therefore the displacement is 0.2941 meters.