Question

Find the surface area. Round to the nearest tenth.12 inI19 in

Answer 1

INFORMATION:

We have the next figure

And we must find its surface area

STEP BY STEP EXPLANATION:

The surface area of a cone is equal to the curved surface area plus the area of the base:

`A=\pi r^2+\pi Lr`

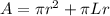
Where, r denotes the radius of the base of the cone, and L denotes the slant height of the cone.

Now, we must calculate L using the right triangle formed

We can use the Pythagorean theorem,

`\begin{gathered} L^2=9^2+12^2 \\ L^2=81+144 \\ L^=√(225) \\ L=15 \end{gathered}`

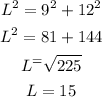
So, having r = 9 in and L = 15 in, we can replace the values in the formula

`\begin{gathered} A=\pi\cdot9^2+\pi\cdot15\cdot9 \\ A=81\pi+135\pi \end{gathered}`

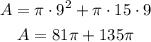
Then, replacing π = 3.14

`\begin{gathered} A=81(3.14)+135(3.14) \\ A=678.2\text{ }in^2 \end{gathered}`

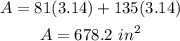
Finally, the surface area of the cone is 678.2 in^2

ANSWER:

678.2 in^2