Question

R is the midpoint of line segment of PQ. PR is 3x + 6 and RQ is 5x - 2.Find the followingX:PR:RO:PQ:

Answer 1

Let's draw a diagram to represent the given problem.

If R is midpoint then PR and RQ are equal by definition of midpoint. So, we can express the following equation.

`\begin{gathered} PR=RQ \\ 3x+6=5x-2 \end{gathered}`

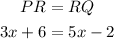
Then, we solve for x. First, we subtract 5x on each side.

`\begin{gathered} 3x-5x+6=5x-5x-2 \\ -2x+6=-2 \end{gathered}`

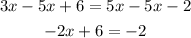
Now, we subtract 6 on each side.

`\begin{gathered} -2x+6-6=-2-6 \\ -2x=-8 \end{gathered}`

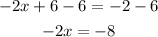
At last, we divide the equation by -2.

`\begin{gathered} (-2x)/(-2)=(-8)/(-2) \\ x=4 \end{gathered}`

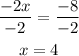
The solution for x is 4.

We use this value to find PR and RQ.

`PR=3x+6=3(4)+6=12+6=18=RQ`

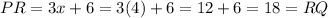
Then, we find PQ.

`PQ=18+18=36`

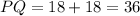
Therefore, PR and RQ are equal to 18 units, and PQ is equal to 36 units.