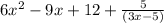Question

Perform the indicated operations on the following polynomials.Divide: 6x3 + 27x - 19x2 - 15 by 3x -5

Answer 1

Step-by-step explanation:

Given;

We are given the polynomial below;

`6x^3+27x-19x^2-15`

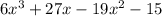
Required;

We are required to divide the polynomial by;

`3x-5`

Step-by-step solution;

We shall apply the synthetic division method of dividing polynomials.

The first step would be to re-arrange the polynomial in standard form. This is shown below;

`6x^3-19x^2+27x-15`

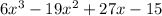
Next step, we list out the coefficients of the polynomial;

`6,-19,27,-15`

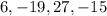
Next step, we identify the zeros of the denominator;

`\begin{gathered} 3x-5=0 \\ \\ 3x=5 \\ \\ x=(5)/(3) \end{gathered}`

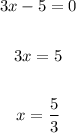
We can now write down the question in synthetic division format;

Next step, we carry down the leading coefficient below the division symbol.

Next step, we multiply this value by the zero of the denominator that is, 5/3.

That gives us;

`6*(5)/(3)=10`

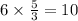
Now we write 10 right under the next coefficient and that is -19. We add both together (-19 + 10 = -9) and write the result below the division symbol. Next we multiply this too by the zero of the denominator and we have;

`-9*(5)/(3)=-15`

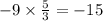
We write this too under the next coefficient and we have;

`27-15=12`

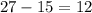
We multiply this too by 5/3 and we have 20. Write this right under the next coefficient and add up and we now have;

`-15+20=5`

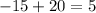
The result we have come up with are the coefficients beneath the division symbol and that is;

`6,-9,12,5`

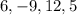
The last number is the remainder and the result of the division carried out will be;

`6x^2-9x+12\text{ }Rem\text{ }5`

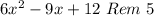
This is otherwise written out as follows;

ANSWER:

`6x^2-9x+12+(5)/((3x-5))`