The formula for determining the volume of a cone is:
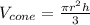
where r = radius and h = height of the cone.
Based on the question, the radius = 30ft, the height = 20ft, and to use π = 3.14.
Let's replace the variables in the formula above with their corresponding numerical value.
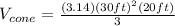
Then, solve.
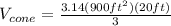
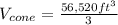
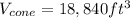
Therefore, the volume of the building is 18, 840 cubic feet.