Question

A ball is thrown vertically upward from the height of 2.5 meters. The height (in meters) of the ball above the ground is modeled by the equation y = -4t2 + 3t + 2.5, where t is the time in seconds from the moment the ball was released. How much time did it take the ball to hit the ground? A ball is thrown vertically upward from the height of 2.5 meters. The height (in meters) of the ball above the ground is modeled by the equation y = -4t2 + 3t + 2.5, where t is the time in seconds from the moment the ball was released. How much time did it take the ball to hit the ground? one of the below is the answer0.45 seconds0.5 seconds1.25 seconds1.85 seconds

Answer 1

We are given that the height of a ball is given by the following equation:

`y=-4t^2+3t+2.5`

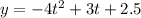
To determine the time it takes the ball to hit the ground we must set the equation to zero, like this:

`-4t^2+3t+2.5=0`

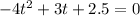
Now, we will multiply both sides by -1:

`4t^2-3t-2.5=0`

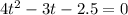
Now, to determine the values of "t" we use the fact that the equation has the following form:

`at^2+bt+c=0`

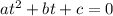
Therefore, its solution is given by the quadratic formula:

`t=(-b\pm√(b^2-4ac))/(2a)`

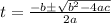
Now, we substitute the values:

`t=(-(-3)\pm√((-3)^2-4(4)(-2.5)))/(2(4))`

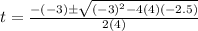
Now, we solve the operations inside the radical:

`t=(3\pm√(49))/(8)`

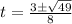
Solving the radical:

`t=(3\pm7)/(8)`

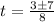
Now, we take the positive value because we want the time to have a positive value:

`t=(3+7)/(8)=(10)/(8)=1.25`

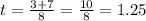
Therefore, it takes the ball 1.25 seconds to reach the ground.