The Solution:
Given that the population of Slim Chance is described by the exponential function below:
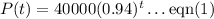
We are required to find the rate at which the population is changing, and also give a numerical rate of change in the population.
By formula, the exponential function is:
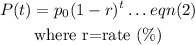
Comparing eqn(1) and eqn(2), we have that:
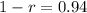
Solving for r in the above equation, we get
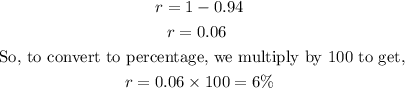
To find the numerical rate of change in the population, we get
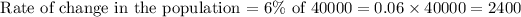
Therefore, the population decreases by 2400 people every year.