Question

For this exercise, use the position function s(t) = −4.9t^2 + 250, which gives the height (in meters) of an object that has fallen for t seconds from a height of 250 meters. The velocity at time t = a seconds is given by lim t→a s(a) − s(t) / a − t . When will the object hit the ground? At what velocity, v, will the object impact the ground?(Note: I saw this question with the answer as t=7.14s and v=-69.972 m/s I plug that in but it’s showing incorrect) please help

Answer 1

First, find the time that it takes for the position to be equal to 0, which represents the moment when the object hits the ground:

`\begin{gathered} s(t)=0 \\ \\ \Rightarrow\quad-4.9t^2+250=0 \\ \\ \Rightarrow\quad4.9t^2=250 \\ \\ \Rightarrow\quad t^2=(250)/(4.9) \\ \\ \Rightarrow\quad t=\sqrt{(250)/(4.9)}=7.14...s \end{gathered}`

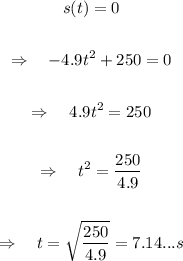
Next, remember that the velocity of an object is the derivative with respect to time of its position, as stated in the text in the form of a limit, which would result in:

`v(t)=-9.8t`

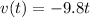
Replace t=7.14s to find the velocity when the object hits the ground:

`v(7.14s)=-9.8*7.14...=-70(m)/(s)`

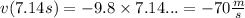
Therefore, the answer is: the object will impact the ground with a velocity of -70m/s.