a) We have to calculate the magnitude M of the earthquake.
We will use the first intensity measure, that is I = 10^5.4*I₀.
We then can calculate the magnitude M as:
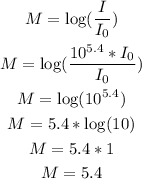
b) Now we will use the revised measure of I = 10^6.2*I₀ to calculate the magnitude:
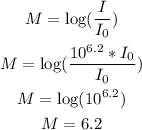
c) We have to calculate how many more intense was the earthquake than originally thought. We can calculate this as the ratio between the actual magnitude (revised) and the original:
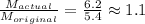
It was 1.1 times more intense (about 10% more intense).
Answer:
a) M = 5.4
b) M = 6.2
c) 1.1 times