From the text, we get two equations that relates the rate of the Smith family sprinkler and the Figueroa family sprinkler. Let's call the rate of water of the Smith family sprinkler "S" and the rate of water of the Figueroa family sprinkler "F".
Since the the Smith family sprinkler was used for 25 hours and the Figueroa family sprinkler was used for 35 hours, and the combined output was 1850L, we have the following equation:
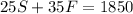
And since the sum of both rates equals 60L/h, we have the following:
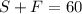
Now, we just have to solve this system.
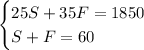
First, we can simplify the first equation by dividing every term by 5.
This lead us to this system

If we multiply the second equation by five, and subract it from the first equation, we get an equation only with F.

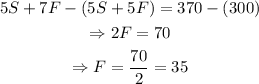
This tell us that the rate of the water output for the Figueroa family sprinkler is 35L/h. With this value, we can just substitute in any equation of our system and get the other rate.
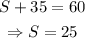
And this is the rate for the Smith family sprinkler. 25L/h.