Question

A chemical company makes two brands of antifreeze. The first brand is 35% pure antifreeze, and the second brand is 60% pure antifreeze. In order to obtain 60 gallons of a mixture that contains 45% pure antifreeze, how many gallons of each brand of antifreeze must be used?First brand Second brand

Answer 1

Given the word problem, we can deduce the following information:

1. The first brand is 35% pure antifreeze, and the second brand is 60% pure antifreeze.

2. The chemical company intended to obtain 60 gallons of a mixture that contains 45% pure antifreeze.

To determine the amount in gallons of each brand of antifreeze, we first let:

x= the amount of 35% pure antifreeze

60-x= the amount of 60% pure antifreeze

Based on the given information, our equation would be:

`0.35x+0.60(60-x)=0.45(60)`

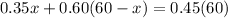
Next, we get the value of x:

`\begin{gathered} 0.35x+0.60(60-x)=0.45(60) \\ \text{Simplify and rearrange} \\ 0.35x+36-0.6x=27 \\ -0.25x+36=27 \\ 0.25x=36-27 \\ 0.25x=9 \\ x=(9)/(0.25) \\ \text{Calculate} \\ x=36\text{ gallons} \end{gathered}`

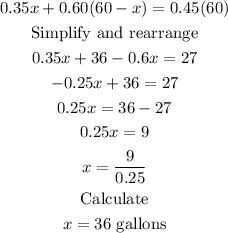
Then, we plug in x=36 into 60-x:

`60-x=60-36=24\text{ gallons}`

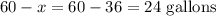
Therefore,

First brand = 36 gallons

Second brand = 24 gallons