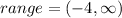Given:
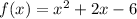
We get two points from the given table.
(-6,14) and (-3,8).
Required:
We need to find the range of (f+g)(x).
Step-by-step explanation:
Consider the equation of the linear function.
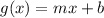
where m is the slope.
Consider the formula to find the slope.
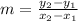
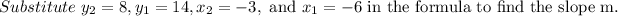
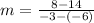
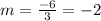
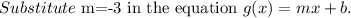

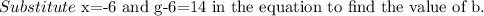
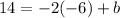
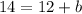
Subtract 12 from both sides of the equation.
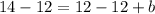
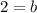
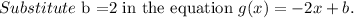
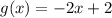
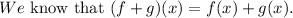
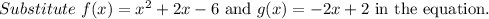
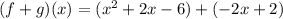
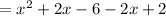
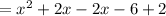
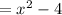
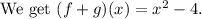
The graph of the function (f+g)(x).
We know that the range of a graph consists of all the output values shown on the y-axis.
The minimum value of the range is -4.
The graph moves upward to infinity.
The maximum value of the range is infinity.
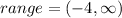
Final answer: