Question

Show the equations in slope intercept form and determine how many solutions does the system of equations have? Explain.2x - 9y = -5 4x - y = 2

Answer 1

first solve each equation for y

`\begin{gathered} 2x-9y=-5 \\ -9y=-5-2x \\ y=(5)/(9)+(2)/(9)x \end{gathered}`

`\begin{gathered} 4x-y=2 \\ -y=2-4x \\ y=-2+4x \end{gathered}`

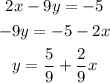
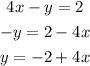
the equations are

`\begin{gathered} y=(5)/(9)+(2)/(9)x \\ \\ y=-2+4x \end{gathered}`

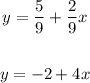
we can substract the equations to remove y

`\begin{gathered} y=(5)/(9)+(2)/(9)x \\ \\ y=-2+4x \\ \\ ---------------- \\ 0=(23)/(9)-(34)/(9)x \end{gathered}`

now solve x

`\begin{gathered} (23)/(9)-(34)/(9)x=0 \\ \\ 23-34x=0 \\ 34x=23 \\ \\ x=(23)/(34) \end{gathered}`

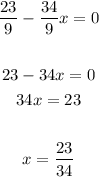
the value of x is 23/34, now replace on any equation to find Y, I will replace on the second

`\begin{gathered} y=-2+4((23)/(34)) \\ \\ y=-2+(46)/(17) \\ \\ y=(12)/(17) \end{gathered}`

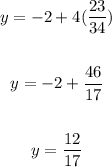
the value of y is 12/17

the solution point is ( 23/34 , 12/17)