Answer:
• 1. y=5x+14
,
• 2. y=5x+30
Explanation:
Given the equation:
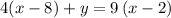
To answer the given questions, first, make y the subject of the given equation.
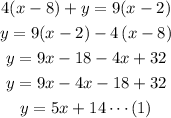
Part 1
We want to find an expression of the form y=ax+b such that the equation has infinitely many solutions.
A system of equations has infinitely many solutions if the two equations in the system simplify to the same line.
Thus, we find an equation that is a multiple of the simplified equation (1) above.
Multiply equation 1 all through by 1.
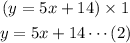
Thus, the system of equations:

This system has infinitely many solutions since they simplify to the same line.
Part 2
We want to find an expression of the form y=ax+b such that the equation has no real solutions.
For a system of equations to have no real solutions, the two lines formed by the equations must be parallel.
This means that they must have the same slope.
In equation 1:
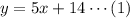
The slope is 5.
Thus, find another equation that also has a slope of 5.
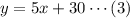
The system of equations below has no real solutions.
![\begin{gathered} y=5x+14\operatorname{\cdots}(1) \\ y=5x+30\operatorname{\cdots}(3) \end{gathered}]()