To find the area of the composite figure, we need to break it apart into known shapes.
We find area of all the broken pieces and sum it to find the area of the whole.
Let's see the composite figure, broken down:
• Region 1 is a trapezoid
,
• Region 2 is another trapezoid but exactly same area as the first
,
• Region 3 is a rectangle
,
• Region 4 is a triangle
Now, let's label the figure with side lengths. The picture is shown below:
Now let's find the area of each region by using respective formulas for areas of shapes we know:
Area of Region 1
Region 1 is a trapezoid and the area will be:
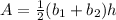
Where
b1 and b2 are the two bases (top and bottom) respectively and h is the height
Given,
b1 = 2
b2 = 6
h = 2
The area is:
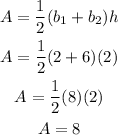
Area of Region 2
This trapezoid is exactly same as the Region 1 trapezoid.
Its area would also be "8".
Area of Region 3
This is a rectangle with length "12" and height "4".
The area is found by multiplying the length and height, thus:
A = 12 * 4 = 48
Area of Region 4
This is a triangle. The area is given by the formula:
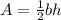
Where
b is the base and h is the height
Given,
b = 12
h = 4
So, we have:
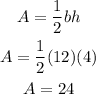
Thus,
The Total Area of the composite figure is:
8 + 8 + 48 + 24 = 88 square units