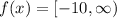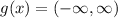Given
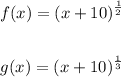
Find
Domain of the function
Step-by-step explanation
Domain of the function is the set of all possible values of x which will given the output value y.
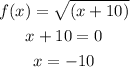
so , domain of the function , f(x) =
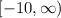
and
as we know that the domain of the function is all real numbers except where the function is undefined.
in this case , there is no real number which makes the function undefined.
so , domain of g(x) is all values of x
so ,
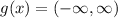
Final Answer
Therefore , the domain of f(x) anf g(x) are