Question

A cooler contains four colas, seven root beers, and four ginger ales. Three people grab a drink at random, one at a time.a) What is the probability that the first person grabs a cola, the second person grabs a ginger ale, and the third person grabs a cola? b) What is the probability that the third person grabs a root beer given that the first two grabbed colas?

Answer 1

Given:

• Number of colas = 4

,

• Number of robot beers = 7

,

• Number of ginger ales = 4

Where:

Total number if drinks = 4 + 7 + 4 = 15

Given that 3 people grab a drink at random, one at a time.

Let's solve for the following:

• (a). What is the probability that the first person grabs a cola, the second person grabs a ginger ale, and the third person grabs a cola?

• Probability the first person grabs a cola is:

`P(first\text{ cola\rparen=}\frac{number\text{ of colas}}{total\text{ number of drinks}}=(4)/(15)`

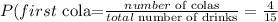
• Probability second person grabs a ginger is:

`P(second\text{ ginger\rparen=}\frac{number\text{ of ginger ales}}{total\text{ number -1}}=(4)/(15-1)=(4)/(14)=(2)/(7)`

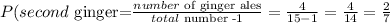
The probability the third prson grabs a cola is:

`P(third\text{ cola\rparen=}(4-1)/(15-2)=(3)/(13)`

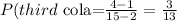
Therefore, the total probability will be:

`\begin{gathered} P=(4)/(15)*(2)/(7)*(3)/(13) \\ \\ P=(4*2*3)/(15*7*13) \\ \\ P=(24)/(1365) \\ \\ P=(8)/(455) \end{gathered}`

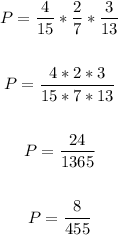
Therefore, the probability that the first person grabs a cola, the second person grabs a ginger ale, and the third person grabs a cola is 8/455.

• (b). What is the probability that the third person grabs a root beer given that the first two grabbed colas?

The probability will be:

`\begin{gathered} P=(4)/(15)*(3)/(14)*(7)/(13) \\ \\ P=(4*3*7)/(15*14*13) \\ \\ P=(84)/(2730) \\ \\ P=(2)/(65) \end{gathered}`

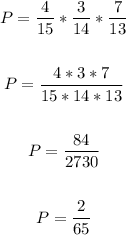
Therefore, the probability that the third person grabs a root beer given that the first two grabbed colas is 2/65.

ANSWER:

• (a). 8/455

• (b). 2/65