Answer:
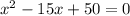
Explanations:
The standard expression for a quadratic equation is expressed as:

If the roots of the equation is a and b, the factors of the equation will be (x-a) and (x-b)
If the roots of the equation is 5 and 10, hence the required factors will be (x - 5) and (x - 10)
Take the product of the factors to determine the required equation
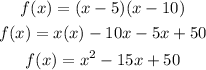
Hence the equation with the roots 5 and 10 is x^2 - 15x + 50 = 0