Question

What is the radius of a sphere with a volume of 36,000 Pi mm3?

Answer 1

The volume of a Sphere was determined using the following formula:

`V=(4)/(3)\pi r^3`

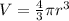
Given that you know the volume of the sphere, you can determine its radius.

First, let's write the formula for r:

- multiply both sides of the equal sign by the reciprocal fraction of 4/3π to leave the r term alone on the left side of the formula:

`V\cdot(3)/(4)\pi=r^3`

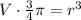
-apply the cubic root to both sides of the equal sign

`\begin{gathered} \sqrt[3]{V\cdot(3)/(4)\pi}=\sqrt[3]{r^3} \\ \sqrt[3]{V\cdot(3)/(4)\pi}=r \end{gathered}`

Replace the expression obtained with the given volume of the sphere:

`\begin{gathered} r=\sqrt[3]{36000\pi\cdot(3)/(4)\pi} \\ r=\sqrt[3]{27000} \\ r=30 \end{gathered}`

The radius of the sphere is 30mm long