Question

QuestionSelect the graph with the final image of ABC after the given sequence of transformations. Rotate ABC90° clockwise about the origin and then reflected over the x-axis.

Answer 1

So first of all we need to list the three points A, B and C so we can properly calculate the transformation:

`\begin{gathered} A=(-3,3) \\ B=(-5,5) \\ C=(-4,6) \end{gathered}`

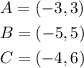
The first transformation we have to perform is a 90° clockwise rotation about the origin. If we perform this rotation on a point (x,y) we get:

`(x,y)\rightarrow(y,-x)`

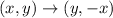
Then we apply this to A, B and C:

`\begin{gathered} A=(-3,3)\rightarrow A^(\prime)=(3,3) \\ B=(-5,5)\rightarrow B^(\prime)=(5,5) \\ C=(-4,6)\rightarrow C^(\prime)=(6,4) \end{gathered}`

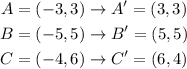
Then we must perform a reflection over the x-axis on the points of triangle A'B'C'. A reflection over the x-axis is achieved by applying this transformation:

`(x,y)\rightarrow(x,-y)`

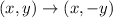
If we transform points A', B' and C' with this we get:

`\begin{gathered} A^(\prime)=(3,3)\rightarrow A^(\prime)^(\prime)=(3,-3) \\ B^(\prime)=(5,5)\rightarrow B^(\prime\prime)=(5,-5) \\ C^(\prime)=(6,4)\rightarrow C^(\prime\prime)=(6,-4) \end{gathered}`

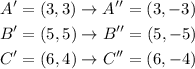
Then if we graph all the three triangles in the same grid we get the following picture:

As you can see this image is the same as the one in option D. This means that the answer to this question is graph D.