Given:
The length of the box is l = 5 inches.
The width of the box is w = 4 inches.
The height of the box is h = 3.5 inches.
The objective is to find the surface area of the box to cover with a wrapper.
Step-by-step explanation:
The general formula to find the surface area of the box is,
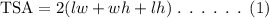
On plugging the given values in equation (1),
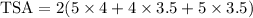
On further solving the above equation,
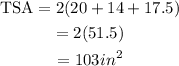
Hence, the required wrapping paper is 103 square inches.