To answer this question, we can see that:
Then, we have that both triangles are similar triangles since the side CB and XY are parallel and then the interior angles are congruent. Then, we can write the next proportions:
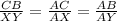
We have that the ratio between CB and XY is:

In other words, we can say that the side CB is twice the measure of side XY or:
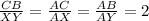
And we can also say that:
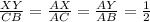
Using these proportions is easy to find the values of AX and AY as follows:
Finding the value of AX
We have that AC = 14cm, then:
![(AX)/(AC)=(1)/(2)\Rightarrow AX=(1)/(2)\cdot AC\Rightarrow AX=(1)/(2)\cdot14\operatorname{cm}\Rightarrow AX=7\operatorname{cm}]()
Finding the value of AY
We have that AB = 18cm, then we have:
![(AY)/(AB)=(1)/(2)\Rightarrow AY=(1)/(2)\cdot AB\Rightarrow AY=(1)/(2)\cdot18\operatorname{cm}\Rightarrow AY=9\operatorname{cm}]()
In summary, therefore, the value for AX = 7cm, and the value for AY = 9cm.