Question

Write a recursive formula for the arithmetic sequence and identify the 8th term.a={8.9, 10.3, 11.7,...}Please share your work/thinking/calculations to earn full credit.

Answer 1

An arithmetic sequence is given. It is required to find the recursive formula and the 8th term.

The given sequence is:

`a=\left\lbrace8.9,10.3,11.7,...\right\rbrace`

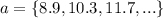
Explanations:

Recall that a recursive formula is a formula in which the next term of a sequence is defined by prior terms.

The recursive formula of an arithmetic sequence is:

`a_n=a_(n-1)+d`

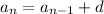
Where n is the number of terms, a₁ is the first term, and d is the common difference of the sequence.

The common difference is the difference between each pair of consecutive terms in an arithmetic sequence.

Hence, the common difference of the given sequence is:

`d=10.3-8.9=1.4`

Substitute the common difference into the recursive formula:

`a_n=a_(n-1)+1.4`

Substitute n=4 into the formula:

`\begin{gathered} a_4=a_(4-1)+1.4 \\ \Rightarrow a_4=a_3+1.4 \end{gathered}`

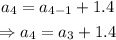
Substitute the third term of the sequence:

`a_4=11.7+1.4=13.1`

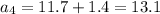
Follow the same procedure of adding the common difference to the previous term to get the next term:

`\begin{gathered} a_5=14.5 \\ a_6=15.9 \\ a_7=17.3 \\ a_8=18.7 \end{gathered}`

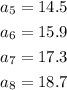
Hence, the 8th term of the sequence is 18.7.

Answers:

The recursive formula of the sequence is:

`a_n=a_(n-1)+1.4`

The 8th term of the sequence is 18.7.