Exponential Growth
The growth of a given variable y with an initial value of Po can be modeled with an exponential function as follows:

Where r is the growth rate and t is the time.
In 2006 (here we assume t = 0), the number of cell phone subscribers was Po = 233 million. We know the number of subscribers increases by r = 6% every year.
a.
With the given information, we can write the exponential function. We must express the rate in decimal, thus r = 6/100 = 0.06.
Our model is expressed as:

This is the exponential model.
The number of subscribers in 2008 can be estimated with our model. The value of t is t = 2008 - 2006 = 2 years:
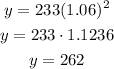
The estimated number of subscribers in 2008 is 262 million.
b.
It's required to find the value of t when y = 278. Substituting in the model function:
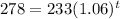
We need to solve for t. Dividing by 233:
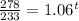
Taking natural logarithms on both sides:
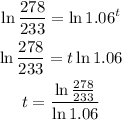
Calculating:
t = 3 years.
In 2009, the number of cell phone subscribers was about 278 million