An equation system has an infinite amount of solution when all the equations that conform it correspond to the same line.
The line shown in the graph has the equation y = 3x - 1
The equation that is equal to the graphed one will be the one that forms a system with an infinite number of solutions.
What you have to do is express each option in slope-intercept form and compare it to the given one:
1.
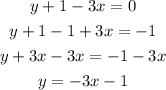
This option does not form a system with infinite solutions with the given equation.
2.
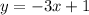
This equation has a different slope and y-intercept than the given line, so it does not form a system with infinite solutions with it.
3.
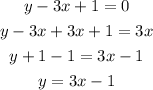
This equation is exactly the same as the one given in the graph, so it will form a system with infinite solutions with it.
4.
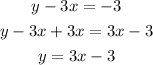
This equation has the same slope but a different y-intercept than the given equation, which means that they are parallel. A system formed between this option and the given line would have no solutions since both lines are parallel.
The only equation which will form a system with infinite equations with the one shown in the graph is number 3. y-3x+1=0