The profit fuction is given as,
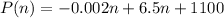
(a):
If the value of n=1000 the profit can be determined as,
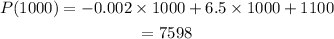
Thus, the required profit is 7598.
(b):
If the value of profit is $6000 then the minimum number of ornamets can be determined as,
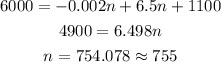
Thus, the required number of minimum ornamets is 755.