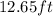Question

The base of a 14 foot ladder is 6 feet from a building if the ladder reaches the flat roof how tall is the building? The height of the building is_ ftThe height of the building is approximately_ft

Answer 1

Step 1. Gather the information that we have and make a diagram.

The length of the ladder is 14 ft, the distance from the base of the ladder to the building is 6 ft and the height of the building is unknown.

We will call this unknown height ''a''.

The following diagram represents the situation:

Step 2. The triangle formed between the floor, the building, and the ladder is a right triangle (it has a 90° angle), this means that we can use the Pythagorean theorem to solve this and find ''a''.

The Pythagorean theorem is represented by the equation:

`a^2+b^2=c^2`

where a and b are the legs of the triangle, and c is the hypotenuse of the triangle (the side opposite to the 90° angle)

In our case,

`\begin{gathered} c=14ft \\ b=6ft \end{gathered}`

And we need to find a.

Step 3. Substituting the known values into the Pythagorean theorem:

`\begin{gathered} a^2+b^2=c^2 \\ a^2+(6ft)^2=(14ft)^2 \end{gathered}`

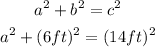
Solving the exponential terms:

`a^2+36ft^2=196ft^2`

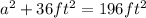
And solving for a^2 by subtracting 36ft^2 to both sides of the equation:

`\begin{gathered} a^2=196ft^2-36ft^2 \\ a^2=160ft^2 \end{gathered}`

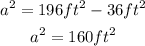
Taking the square root of both sides and simplifying:

`\begin{gathered} \sqrt[]{a^2}=\sqrt[]{160ft^2} \\ \\ a=\sqrt[]{16\cdot10}ft \\ \\ a=4\sqrt[]{10}ft \end{gathered}`

This result can also be represented as a decimal number:

`a=4\sqrt[]{10}ft\approx12.65ft`

Answer:

The height of the building is

`4\sqrt[]{10}ft`

The height of the building is approximately

`12.65ft`