1 Answer

Koenyn · Answer 1 · 2023-08-28T19:05:46+0000

To find the arc length we need to know the angle subtended by the arc.

From the diagram we notice that angle MNK is of 180°.

We also notice that:

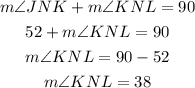
$\begin{gathered} m\angle JNK+m\angle KNL=90 \\ 52+m\angle KNL=90 \\ m\angle KNL=90-52 \\ m\angle KNL=38 \end{gathered}$

Then the angle subtended by the arc MKL is 218°.

Now that we know this we need to remember that the arc length is given by:

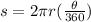
$s=2\pi r((\theta)/(360))$

in this case the radius is 3 ft (The radius is half the diameter) then we have that:

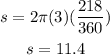
$\begin{gathered} s=2\pi(3)((218)/(360)) \\ s=11.4 \end{gathered}$

Therefore the arc length is 11.4 ft.

Please log in or register to add a comment.