Given in the question:
a.) A group of 12 students and 3 teachers pay $72 for admission to a private research center.
b.) Another group of 14 students and 4 teachers pay $87.
Let,
x = Cost per student
y = Cost per teacher
Let's interpret the scenario of given a and b into an equation. These equations will be the linear systems to be used in getting the cost.
Given a: A group of 12 students and 3 teachers pay $72 for admission to a private research center.
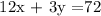
Given b: Another group of 14 students and 4 teachers pay $87.
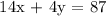
Conclusion: The linear systems you would use to find the cost of one student ticket and one teacher ticket are 12x + 3y = 72 and 14x + 4y = 87.