A reflection across the x-axis is the same as applying the following to all points:
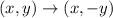
Now, we can apply this to all points of the quadrilateral:
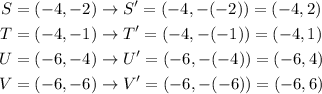
So, the image quadrilateral have the following points:
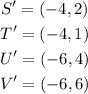
Now, we need to look at which picture have these points. These points all have negative x and positive t, so, the whole quadrilateral is on the second quadrant, the one on top to the left.
So, the two firstr alternatives are the only possible.
Now, if we see the first figure, we can see that T' is on the coordinates (-4, 1), which is exactly what we have got.
On the second image, though, the T' is at coordinates (-6, -6), which is not what we have got, so it can't be the second picture.
So, the correct picture is:
Which is the top left.