Question

A committee must be formed with 3 teachers and 7 students. If there are 6 teachers tochoose from, and 10 students, how many different ways could the committee bemade?

Answer 1

In the selection, the order doesn't matter, then you could use a combination. The formula is:

`C(n,r)=(n!)/(r!(n-r)!)`

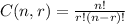
Where n is the number of things to choose from and r is the amount we choose.

Then if there are 6 teaches and the committee must be formed with 3 of then, the combinations are:

`\begin{gathered} C(6,3)=(6!)/(3!(6-3)!) \\ C(6,3)=(6!)/(3!(3)!) \\ C(6,3)=20 \end{gathered}`

And also there are 10 students and the committee must be formed by 7 of them, then the combinations are:

`\begin{gathered} C(10,7)=(10!)/(7!(10-7)!) \\ C(10,7)=(10!)/(7!(3)!) \\ C(10,7)=120 \end{gathered}`

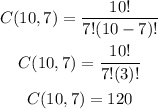
And finally, the total number of ways the committee could be made is:

`C(6,3)* C(10,7)=20*120=2400`

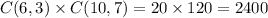
Answer: 2400 ways