Given
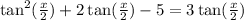
Find
Value of x that makes the equation true and what step will she take first
Step-by-step explanation
to find the value of x , the first step we use
subtract
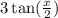
from both sides
on subtraction , we obtain
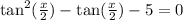
now ,
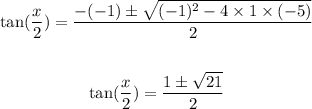
Final Answer
The correct option is C.